skyitachi's blogann-benchmarks中hnsw简单解读 2024-07-23

hnswlib和faiss_hnsw在ann-benchmark中的参数解读

benchmark链接
只需要关注hnswlib和hnsw(faiss) 即可

声明

  • 数据集: sift-128-euclidean数据集(向量的维度是128)
  • k-nn的k是10
  • hnswlib和faiss_hnsw的benchmark都是基于单线程的

benchmark的细节点说明

  1. hnswlib中有相同图例的点, eg：Parameters: hnswlib ({'M': 12, 'efConstruction': 500}) 这样得点标记了好几个，但是QPS和Recall都不相同,
    原因在于hnswlib的benchmark配置中有query-args参数

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    // ann_benchmarks/algorithms/hnswlib/config.yml
    float:
      any:
      - base_args: ['@metric']
        constructor: HnswLib
        disabled: false
        docker_tag: ann-benchmarks-hnswlib
        module: ann_benchmarks.algorithms.hnswlib
        name: hnswlib
        run_groups:
          M-12:
            arg_groups: [{M: 12, efConstruction: 500}]
            args: {}
            query_args: [[10, 20, 40, 80, 120, 200, 400, 600, 800]]
    	...

    // query_args 对应了 hnswlib/module.py中的set_query_arguments函数的参数

        def set_query_arguments(self, ef):
            self.p.set_ef(ef)

  2. hnswlib中set_ef和faiss_hnsw中设置efSearch的效果是一样的, faiss中的图例就标注了efSearch(ef) ,"faiss ({'M': 12, 'efConstruction': 500}, ef: 80)

  3. efSearch不影响build，所以在Recall/Build time的图上hnswlib就没有”重复”的点了

hnswlib和faiss_hnsw的性能表现

主要看recall和build的表现

ann-benchmark中的表现

参考ann-benchmark的论文，他们运行的硬件环境是: Amazon EC2 c5.4xlarge instances that are equipped with Intel Xeon Platinum 8124M CPU (16 cores available, 3.00 GHz, 25.0MB Cache) and 32GB of RAM running Amazon Linux.

ann-benchmarks网站上的benchmark如下:

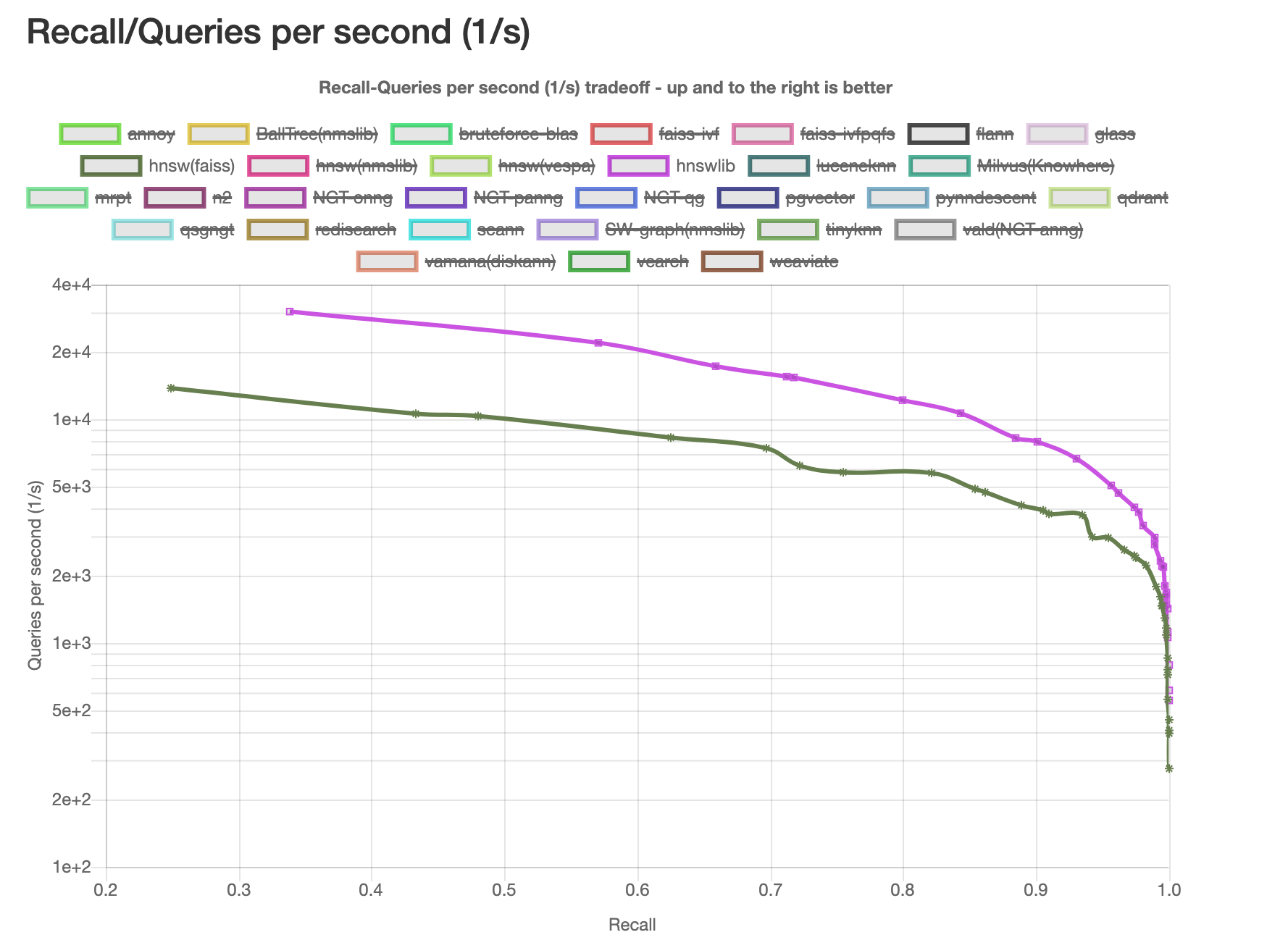
Recall

说明:

  1. 整体QPS随着recall的上升成指数级的下降 (两者都是)

  2. 相同召回率的情况下，hnswlib的QPS要高一点, 由于faiss标注了ef(efSearch)但是hnswlib没有标注，所以比较起来不太直观，后面我在本地自己跑的时候给hnswlib带上了ef参数，这样就更加直观了

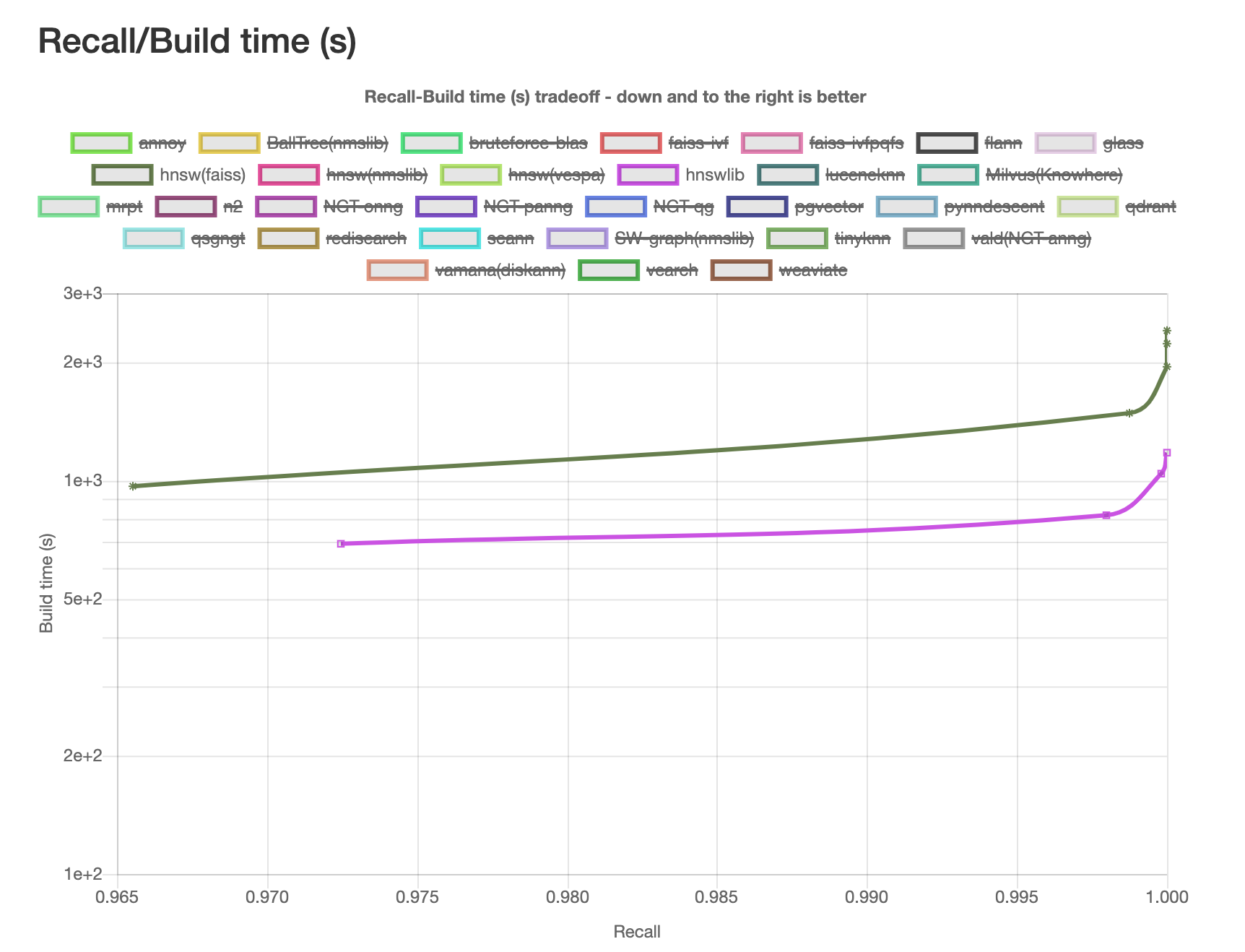
Build Index Time

说明: 1. Build Index Time也是hnswlib占优

本地的表现

硬件环境: AMD Ryzen 5 3600 (3.6G Hz), 6 core 12 threads, 32GB of RAM running Ubuntu 24.04

这里我修改了ann-benchmarks中hnswlib的环境和在efConstruction=200和500的情况下比较hnswlib的表现

1
2
3
4
5
6
7
8
9
// ann_benchmarks/algorithms/hnswlib/config.yml
FROM ann-benchmarks

# RUN apt-get install -y python-setuptools python-pip
RUN pip3 install pybind11 numpy setuptools hnswlib==0.8.0

# RUN cd hnsw/python_bindings; python3 setup.py install

RUN python3 -c 'import hnswlib'

Recall & QPS 表现

关于recall 我们更需要关注是否通过参数配置到足够高的精度，我这里以0.99的recall作为基础，主要比较在0.99以上的召回率条件下(qps > 2000)，两种算法实现的qps及其对应的参数

algorithm parameters k-nn(recall) qps build(s) indexsize(kb)
faiss_hnsw faiss ({‘M’: 24, ‘efConstruction’: 500}, ef: 80) 0.99031 2561.923162412995 1458.773098230362 794864.0
faiss_hnsw faiss ({‘M’: 16, ‘efConstruction’: 500}, ef: 120) 0.99347 2194.419076982479 1285.849939107895 732492.0
faiss_hnsw faiss ({‘M’: 36, ‘efConstruction’: 500}, ef: 80) 0.99314 2191.7604350595634 1585.1033165454865 888936.0
faiss_hnsw faiss ({‘M’: 48, ‘efConstruction’: 500}, ef: 80) 0.99411 2077.6779248107487 1667.5446255207062 982148.0
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 200}, ef: 80) 0.9901500000000001 3731.2651844102425 496.65849924087524 1150800.0
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 200}, ef: 80) 0.9902599999999999 3616.44180507205 513.7249546051025 1400632.0
hnswlib hnswlib ({‘M’: 36, ‘efConstruction’: 500}, ef: 80) 0.99308 3571.6658501707066 1156.385510444641 931660.0
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 200}, ef: 120) 0.9939 3314.9200264352426 426.75320744514465 838564.0
hnswlib hnswlib ({‘M’: 48, ‘efConstruction’: 500}, ef: 80) 0.99433 3290.7135482210724 1246.9214706420898 1026148.0
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 500}, ef: 80) 0.9946999999999999 3153.6867226554614 1276.8294219970703 1146332.0
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 500}, ef: 120) 0.9955999999999999 3139.927141602247 1008.0483357906342 838676.0
hnswlib hnswlib ({‘M’: 12, ‘efConstruction’: 200}, ef: 200) 0.9920199999999999 3100.2119285498034 313.95580410957336 745664.0
hnswlib hnswlib ({‘M’: 12, ‘efConstruction’: 500}, ef: 200) 0.99271 3040.3355289720653 709.9178235530853 745132.0
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 500}, ef: 80) 0.9949 3036.296166689699 1317.8283751010895 1400940.0
hnswlib hnswlib ({‘M’: 36, ‘efConstruction’: 200}, ef: 120) 0.99544 2873.9128879689624 466.08784890174866 931436.0
hnswlib hnswlib ({‘M’: 48, ‘efConstruction’: 200}, ef: 120) 0.9956799999999999 2690.4460742892884 482.9417383670807 1025096.0
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 200}, ef: 120) 0.99576 2671.663602183599 496.65849924087524 1150800.0
hnswlib hnswlib ({‘M’: 36, ‘efConstruction’: 500}, ef: 120) 0.99753 2612.247989122775 1156.385510444641 931660.0
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 200}, ef: 120) 0.99588 2581.161300550079 513.7249546051025 1400632.0
hnswlib hnswlib ({‘M’: 16, ‘efConstruction’: 200}, ef: 200) 0.9962 2565.1980331237614 364.242990732193 778360.0
hnswlib hnswlib ({‘M’: 48, ‘efConstruction’: 500}, ef: 120) 0.9979100000000001 2394.6802442922076 1246.9214706420898 1026148.0
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 500}, ef: 120) 0.9980800000000001 2282.691070497442 1276.8294219970703 1146332.0
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 500}, ef: 120) 0.99821 2188.4360442789643 1317.8283751010895 1400940.0
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 200}, ef: 200) 0.99818 2166.896152958348 426.75320744514465 838564.0
hnswlib hnswlib ({‘M’: 8, ‘efConstruction’: 200}, ef: 400) 0.99244 2138.951169866413 256.2939279079437 715140.0
hnswlib hnswlib ({‘M’: 8, ‘efConstruction’: 500}, ef: 400) 0.9936 2124.6338197635687 588.7308986186981 715372.0
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 500}, ef: 200) 0.9989100000000001 2017.995520316913 1008.0483357906342 838676.0

Build Index Time

algorithm parameters indexsize build
hnswlib hnswlib ({‘M’: 8, ‘efConstruction’: 200}, ef: 400) 715140.0 256.2939279079437
hnswlib hnswlib ({‘M’: 12, ‘efConstruction’: 200}, ef: 200) 745664.0 313.95580410957336
hnswlib hnswlib ({‘M’: 16, ‘efConstruction’: 200}, ef: 200) 778360.0 364.242990732193
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 200}, ef: 120) 838564.0 426.75320744514465
hnswlib hnswlib ({‘M’: 36, ‘efConstruction’: 200}, ef: 120) 931436.0 466.08784890174866
hnswlib hnswlib ({‘M’: 48, ‘efConstruction’: 200}, ef: 120) 1025096.0 482.9417383670807
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 200}, ef: 120) 1150800.0 496.65849924087524
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 200}, ef: 80) 1400632.0 513.7249546051025
hnswlib hnswlib ({‘M’: 8, ‘efConstruction’: 500}, ef: 400) 715372.0 588.7308986186981
hnswlib hnswlib ({‘M’: 12, ‘efConstruction’: 500}, ef: 200) 745132.0 709.9178235530853
hnswlib hnswlib ({‘M’: 24, ‘efConstruction’: 500}, ef: 120) 838676.0 1008.0483357906342
hnswlib hnswlib ({‘M’: 36, ‘efConstruction’: 500}, ef: 120) 931660.0 1156.385510444641
hnswlib hnswlib ({‘M’: 48, ‘efConstruction’: 500}, ef: 120) 1026148.0 1246.9214706420898
hnswlib hnswlib ({‘M’: 64, ‘efConstruction’: 500}, ef: 120) 1146332.0 1276.8294219970703
faiss_hnsw faiss ({‘M’: 16, ‘efConstruction’: 500}, ef: 120) 732492.0 1285.849939107895
hnswlib hnswlib ({‘M’: 96, ‘efConstruction’: 500}, ef: 120) 1400940.0 1317.8283751010895
faiss_hnsw faiss ({‘M’: 24, ‘efConstruction’: 500}, ef: 80) 794864.0 1458.773098230362
faiss_hnsw faiss ({‘M’: 36, ‘efConstruction’: 500}, ef: 80) 888936.0 1585.1033165454865
faiss_hnsw faiss ({‘M’: 48, ‘efConstruction’: 500}, ef: 80) 982148.0 1667.5446255207062

说明

1.efConstruction越小，build 耗费时间越小，牺牲的精确性可以通过加大ef来弥补, 要想获取最佳性能需要对M，efConstruction, ef这三个参数进行平衡
2.indexsize 只和M有关系
3.整体而言，hnswlib的性能仍然要比faiss的hnsw的要好一点, 两者差距不大
4.efConstruction=200的情况下通过适当调大ef也能实现较高的召回率，也不会带来性能损失，但是对Build Index Time 会有较大的提升

其他细节指标解读

  1. ann-benchmarks中通过python data_export.py可以得出详细的指标数据, 其中有两列epsilon, largeepsilon
    这里其实对应得是在算recall的时候，允许的距离误差大小(使用euclidean距离，就是向量召回的点和实际的knn的点距离误差), epsilon 是0.01， largeepsilon, 允许的误差越大，对应的recall 就越高, 论文中的实际公式如下:

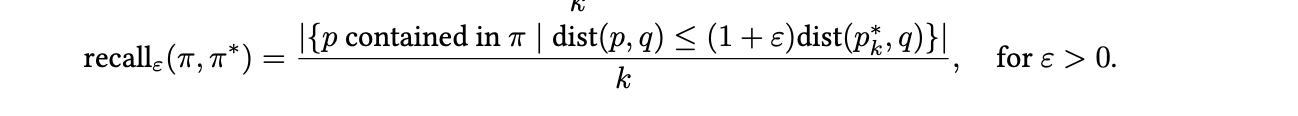
  1. indexsize在graph base的算法中都挺大的，不过整体上hnswlib的更小一点

总结

  1. 这里列举都是在特定数据集下的表现，事实上不同数据集下不同类型的算法表现不尽相同，hnswlib不是在任何情况下的表现都由于faiss_hnsw， 那在实际的生产环境中，还是需要对不同的算法进行benchmark，从而得出更好的参数和选出更好的算法

  2. ann-benchmarks的论文指出虽然graph-based的算法在rand-euclidean的数据集下性能还不如faiss-ivf，但是在实际的数据集上，往往会有所谓的global structure出现，graph based的算法一般都是更好的选择，graph based中的hnsw也是更好的选择

  3. ann-benchmarks也指出如果使用GPU的话，graph based的算法不如ivf这种简单的算法

▲